本帖最后由 ruhuasiyu 于 2016-8-16 20:45 编辑
本文受 http://www.mcbbs.net/thread-565887-1-1.html @林扬骐 启发,但是我觉得原来的作者原理上讲的可能不是很清楚,而且算法(速度)也慢了。
Bezier曲线
首先我就不贴那两张图了。这样的曲线叫做Bezier曲线,n+1个点控制的我们称为n阶Bezier曲线,因为这条曲线的方程式n次的。
例如 n=2 时,对应的曲线一定是抛物线。

过程我不作推导,n次Bezier曲线的方程以向量形式为

特别地, n=2 时为

例子和命令
以 P_0=(0,0,0), P_1=(7,6,-10), P_2=(10,1,-3) 为例
令步数为 N=100, s=100 t, 则
P(s)-P(s-1)=(-0.0008,-0.0022,0.0034)s+(0.1404,0.1211,-0.2017).
我们现在来实现它。首先召唤两个雪球 a 和 b:
复制代码
然后放置 3 个命令方块, 依次为循环型、连锁型条件保持开启、连锁型条件保持开启并输入命令
复制代码
如此第 s 步的时候有 s 个雪球 b,每个雪球 b 将雪球 a 移动 (-0.0008,-0.0022,0.0034),再加上第一个命令的 (0.1404,0.1211,-0.2017), 因此共移动
所以从开始到第 s 步共移动 P(s)-P(0)=P(s),我们成功将雪球 a 移动至 Bezier 曲线上的第 s 的拟合点。

计算公式
对于一般的3个控制点 P_0=(0,0,0), P_1=(a,b,c), P_2=(d,e,f), 设步数为 N,计算出
复制代码
将其代入上述两个 execute 命令的相对坐标即可。
如果需要的话可以加一个循环次数的限制,利用计分板即可,原帖中有提及,这里回忆一下:先生成一个记分板
复制代码
再设置循环次数为 100 次
复制代码
在原来的命令方块前方和后方各添加
复制代码
设置命令方块模式如图

对于n阶Bezier曲线,设步长为 N,将s=Nt 代入公式中计算出 P(s),
然后计算 P(s)-P(s-1) 得到 s 的 n-1 阶多项式,将其从低次到高次的坐标依次代入
复制代码
即可。算法速度为 O(N^n),上述例子大约需执行5000次,时长约数秒。
这是用4条Bezier曲线拟合得到的圆

OOC生成器
如果你觉得上述过程不能理解,你可以直接打开下面的网页,输入控制点的绝对坐标和拟合点的个数,即可生成一条命令,然后将该命令复制到命令方块中执行即可,最后敲到多余的方块。
http://zsx.blog.ustc.edu.cn/wp-c ... 2016/08/bezier.html
每次画完之后请输入
复制代码
将雪球的名字去掉,然后再进行下一条曲线的生成。删除上一次生成的曲线只需
复制代码
删除所有曲线输入
复制代码
因为这几条命令比较简单我就没加到OOC里面了。
以下是利用OOC得到的控制点为 (0,20,0), (0,20,20), (20,20,20) 得到的近似1/4圆。

在文章结尾新增了单指令工具,这样不用计算只需要输入控制点即可得到命令。
本文受 http://www.mcbbs.net/thread-565887-1-1.html @林扬骐 启发,但是我觉得原来的作者原理上讲的可能不是很清楚,而且算法(速度)也慢了。
Bezier曲线
首先我就不贴那两张图了。这样的曲线叫做Bezier曲线,n+1个点控制的我们称为n阶Bezier曲线,因为这条曲线的方程式n次的。
例如 n=2 时,对应的曲线一定是抛物线。

过程我不作推导,n次Bezier曲线的方程以向量形式为

特别地, n=2 时为
例子和命令
以 P_0=(0,0,0), P_1=(7,6,-10), P_2=(10,1,-3) 为例
P=(-4t^2+14t, -11t^2+12t, 17t^2-20t)
令步数为 N=100, s=100 t, 则
P(s)-P(s-1)=(-0.0008,-0.0022,0.0034)s+(0.1404,0.1211,-0.2017).
我们现在来实现它。首先召唤两个雪球 a 和 b:
- summon Snowball ~10 ~5 ~10 {CustomName:"a",CustomNameVisible:1,NoGravity:1}
- summon Snowball ~10 ~5 ~10 {CustomName:"b",CustomNameVisible:1,NoGravity:1}
然后放置 3 个命令方块, 依次为循环型、连锁型条件保持开启、连锁型条件保持开启并输入命令
- tp @e[name=a] ~0.1404 ~0.1211 ~-0.2017
- execute @e[name=b] ~ ~ ~ tp @e[name=a] ~-0.0008 ~-0.0022 ~0.0034
- execute @e[name=a] ~ ~ ~ summon Snowball ~ ~ ~ {CustomName:"b",CustomNameVisible:1,NoGravity:1}
如此第 s 步的时候有 s 个雪球 b,每个雪球 b 将雪球 a 移动 (-0.0008,-0.0022,0.0034),再加上第一个命令的 (0.1404,0.1211,-0.2017), 因此共移动
(-0.0008,-0.0022,0.0034)s+(0.1404,0.1211,-0.2017)=P(s)-P(s-1)。
所以从开始到第 s 步共移动 P(s)-P(0)=P(s),我们成功将雪球 a 移动至 Bezier 曲线上的第 s 的拟合点。

计算公式
对于一般的3个控制点 P_0=(0,0,0), P_1=(a,b,c), P_2=(d,e,f), 设步数为 N,计算出
- (2a(N+1)-d)/N^2, (2b(N+1)-e)/N^2, (2c(N+1)-f)/N^2,
- (2d-4a)/N^2, (2e-4b)/N^2, (2f-4c)/N^2,
将其代入上述两个 execute 命令的相对坐标即可。
如果需要的话可以加一个循环次数的限制,利用计分板即可,原帖中有提及,这里回忆一下:先生成一个记分板
- scoreboard objectives add temp dummy
再设置循环次数为 100 次
- scoreboard players set #n temp 100
在原来的命令方块前方和后方各添加
- scoreboard players test #n temp 1 10000
- scoreboard players remove #n temp 1
设置命令方块模式如图

对于n阶Bezier曲线,设步长为 N,将s=Nt 代入公式中计算出 P(s),
然后计算 P(s)-P(s-1) 得到 s 的 n-1 阶多项式,将其从低次到高次的坐标依次代入
- tp @e[name=a] ~这里 ~这里 ~这里
- execute @e[name=b] ~ ~ ~ tp @e[name=a] ~这里 ~这里 ~这里
- execute @e[name=b] ~ ~ ~ execute @e[name=b] ~ ~ ~ tp @e[name=a] ~这里 ~这里 ~这里
- ……
- 直到 n-1 个 execute @e[name=b] ~ ~ ~ …… execute @e[name=b] ~ ~ ~ tp @e[name=a] ~这里 ~这里 ~这里
即可。算法速度为 O(N^n),上述例子大约需执行5000次,时长约数秒。
这是用4条Bezier曲线拟合得到的圆

OOC生成器
如果你觉得上述过程不能理解,你可以直接打开下面的网页,输入控制点的绝对坐标和拟合点的个数,即可生成一条命令,然后将该命令复制到命令方块中执行即可,最后敲到多余的方块。
http://zsx.blog.ustc.edu.cn/wp-c ... 2016/08/bezier.html
每次画完之后请输入
- entitydata @e[type=Snowball] {CustomName:""}
将雪球的名字去掉,然后再进行下一条曲线的生成。删除上一次生成的曲线只需
- kill @e[type=Snowball,name=a]
- kill @e[type=Snowball,name=b]
删除所有曲线输入
- kill @e[type=Snowball]
因为这几条命令比较简单我就没加到OOC里面了。
以下是利用OOC得到的控制点为 (0,20,0), (0,20,20), (20,20,20) 得到的近似1/4圆。

这玩意可以拿来当装饰,并木有实际意义~
这都是高科技,
{:10_496:}虽然我用不到 但是好厉害
把雪球换成带着方块的盔甲架就能做彩虹了23333
初三表示看不懂乱七八糟的公式了
我看了一下这个帖子,难道说这个数字,是你自己打进去而不是通过cb阵列自行计算的吗?
初二党表示智商不够。
敢问Lz学历几何?
敢问Lz学历几何?
可以做太极Get
都用到高中的知识了= =
pylsdani 发表于 2016-8-14 16:41
这玩意可以拿来当装饰,并木有实际意义~
你可以将雪球替换成方块来盖建筑
乙烯_中国 发表于 2016-8-14 19:20
我看了一下这个帖子,难道说这个数字,是你自己打进去而不是通过cb阵列自行计算的吗? ...
首先我觉得只是小学数学,拿计算器算一下就好了嘛
当然也可以用计分板算,不过总得有一个初始的输入,将曲线的参数带进去
ruhuasiyu 发表于 2016-8-15 12:39
首先我觉得只是小学数学,拿计算器算一下就好了嘛
当然也可以用计分板算,不过总得有一个初始的输入,将 ...
向量都用矩阵表示了还是小学数学?
本帖最后由 林扬骐 于 2016-8-15 19:26 编辑
其实意思都差不多,不过这个这个帖子貌似更清楚明了些XD
lz你家什么电脑啊为什么二次曲线只要数秒啊我家电脑都要将近一分钟我当初为了更易理解改过一次自己结果发现好像更不容易理解了然而改不回来了
其实意思都差不多,不过这个这个帖子貌似更清楚明了些XD
林扬骐 发表于 2016-8-15 04:23
其实意思都差不多,不过这个这个帖子貌似更清楚明了些XD
lz你家什么电脑啊为什么二次曲线只要数秒啊我家 ...
你每次都在原点召唤a,而我是在b处召唤a,因此我每次只需要平移
P(s)-P(s-1)
这么多就可以了,这样做一次差分后就从二次变为线性,总复杂度就从 O(n^3) 变成了 O(n^2),自然快多了。
不过我试了三次曲线的情形也没有你说的那么慢,难道是因为你用的药水云导致的?
ps 我用的是陈年老笔记本电脑,装两个 mod 就卡的那种。
ruhuasiyu 发表于 2016-8-15 19:29
你每次都在原点召唤a,而我是在b处召唤a,因此我每次只需要平移
P(s)-P(s-1)
这么多就可以了,这样做一次 ...
(回去继续看了下自己的帖子,然后又自己算了一下)嘛,的确,如果是“n-(n-1)”的方法可以少一个次方
(当时也有想过使用从n-1到n的方法,但是发现:太!难!算!了!于是就没有再考虑,现在才发现可以降阶)
高科技666,表示看不懂【捂脸
乙烯_中国 发表于 2016-8-15 10:20
我看了一下这个帖子,难道说这个数字,是你自己打进去而不是通过cb阵列自行计算的吗? ...
我在结尾加了一个计算工具来得到OOC,这样就不用计算啦
咳咳,突然想到,如果有生成器的话,直接在生成器内部运算后直接summon就可以了吧(这样只要1秒)
林扬骐 发表于 2016-8-21 12:23
咳咳,突然想到,如果有生成器的话,直接在生成器内部运算后直接summon就可以了吧(这样只要1秒) ...
哈哈,确实。
但其实我觉得可以不用外部工具,直接在内部检测实体坐标,加入记分板做运算,再直接在内部绘制。
是OOC有BUG还是我版本不对
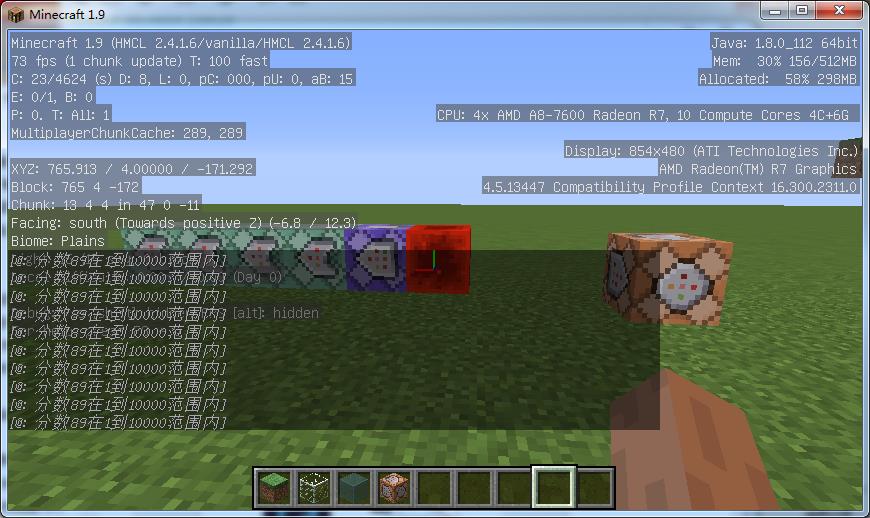

OOC指令


OOC指令
本帖最后由 ruhuasiyu 于 2017-4-15 19:05 编辑
额,不清楚啊!网页没维护,代码可能有误。
最好自己算一下吧
我现在没时间,等迟些我看看代码测试一下
FHC红石 发表于 2017-4-15 18:57
是OOC有BUG还是我版本不对
额,不清楚啊!网页没维护,代码可能有误。
最好自己算一下吧

我现在没时间,等迟些我看看代码测试一下
ruhuasiyu 发表于 2017-4-15 19:04
额,不清楚啊!网页没维护,代码可能有误。
最好自己算一下吧
好吧可能是无重力标签失效了……换成1.10就好了
什么东西看不懂啊
看到这里,我不禁潸然泪下,拿起了小学数学课本...