本帖最后由 ItIsEnderman 于 2020-8-29 10:07 编辑
傅里叶变换给你画画……画圈圈
就这么个小玩意,搞了我两个星期
想了一晚上觉得疏漏还是不少,有一段打算整段重写。
https://www.bilibili.com/blackboard/newplayer.html?playlist=false&crossDomain=1&aid=669294877&page=1
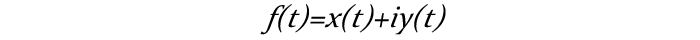
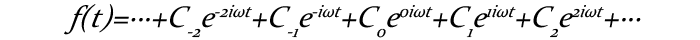
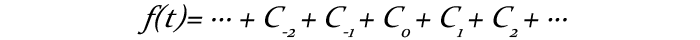

复制代码
复制代码

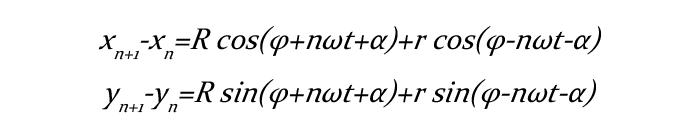
 SVG椭圆解析的doc.zip
(309.6 KB, 下载次数: 0)
SVG椭圆解析的doc.zip
(309.6 KB, 下载次数: 0)
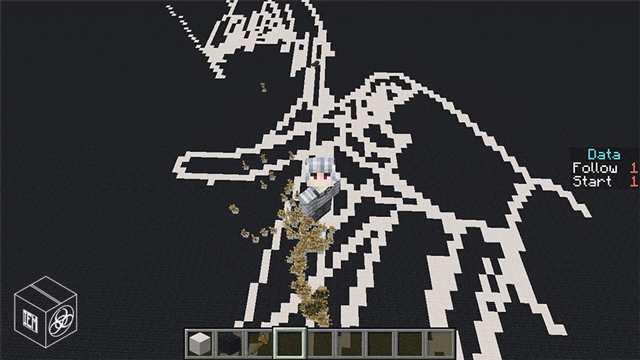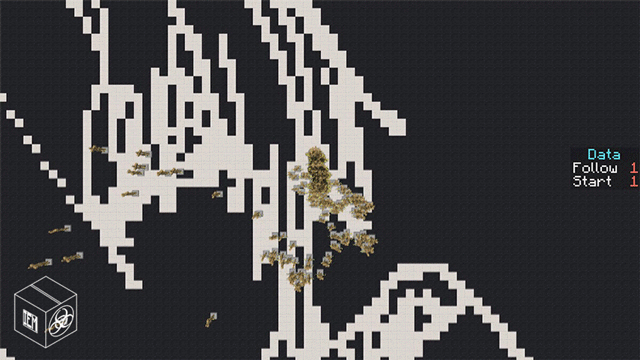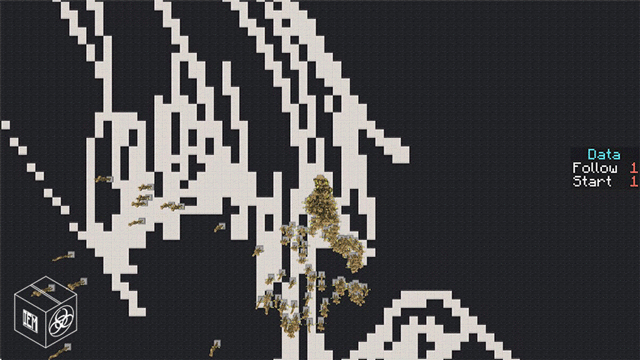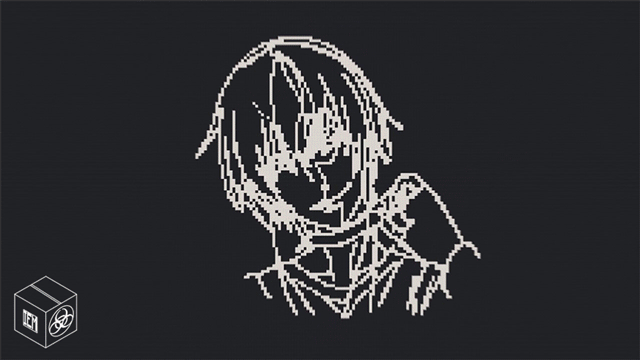
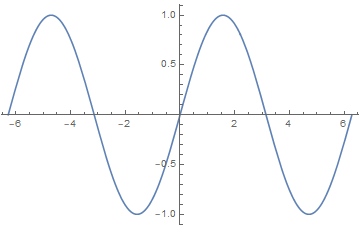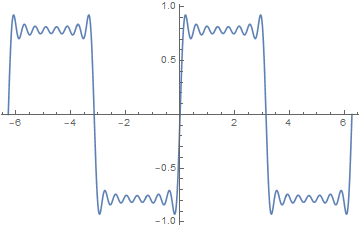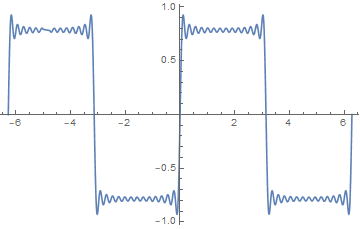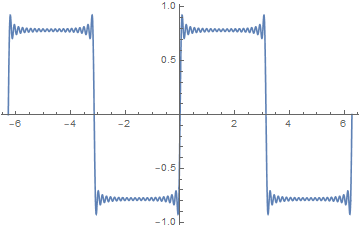
可视化的吉布斯效应,几个月前我的签名档GIF,注意突起的尖端:
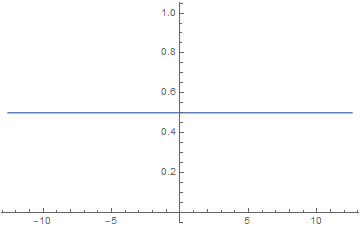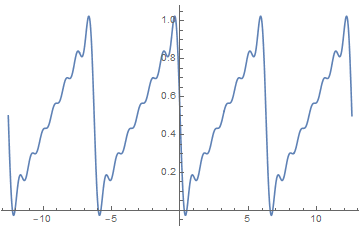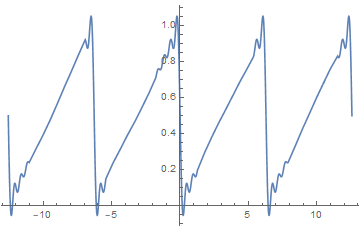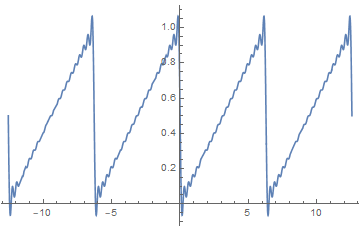
该程序生成数据包的指令说明:
来自群组: Bone Studio就这么个小玩意,搞了我两个星期
想了一晚上觉得疏漏还是不少,有一段打算整段重写。
创作动力直接来自@00ll00 此前提供的“傅里叶本轮法”。因为注意到那个M脚本只能解析M L H V这几个基础SVG指令(看沙发,原因是作者放错文件了,,,),于是我就把贝塞尔曲线和椭圆弧线的也做进去了。我个人是写代码实现的,结果代码三天,修Bug快10天……
好歹这个自己证明一遍数学上成立这个过程也救了我电路课一命,不然一堆的定理压根理解不了
效果展示
最开始为了调试而画了个猫猫头
https://www.bilibili.com/blackboard/newplayer.html?playlist=false&crossDomain=1&aid=669294877&page=1
一方通行用一方通行画一方通行
(300对向量搞的帧数跳跳森的)

实现原理
要知道其实现原理,那就要知道它的数学原理。我们高中时就应该接触过“复平面”这个概念。设我们有一有限长曲线,其解析式F(x,y)=0,那么我们可以求得它的参数方程x=x(t)和y=y(t),并且根据曲线的“有限长”性质,强制定义x=x(t)和y=y(t)均为周期函数(which means,当时间取无限长时,曲线将会被不断重复绘制)。现在我们将y轴转化为复平面的虚轴,这时问题直接转化为复变函数(草)领域内的问题:
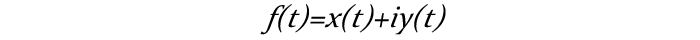
U1S1不要因为复变函数四个字就望风而逃了,很多定理复数实数通用的,你去猜一个定理实数复数通用,八成猜的是对的。
好了回到正题。那么这样一来x(t)+iy(t)也是个周期函数。再说我们的目的是将F(x,y)=0用很多个相互环绕旋转的圈圈进行拟合。我们这里将时间变化设置为线性变化(不然在MC里会占用更大的资源),定义拟合曲线函数和原曲线拥有相同的周期,那么在复平面内我们的拟合曲线方程为:
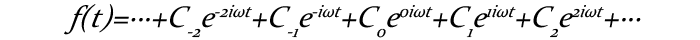
如果你间断点取值得当的话(建议你连续),定义域内拟合曲线解析式应当收敛于原函数。使用很多enωt这玩意,你问问欧拉公式就知道为啥了。解析式中Cn均为复数。
这时令t=0,就得到:
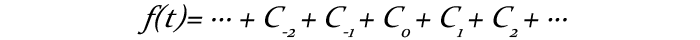
如果回到实数领域的平面,那么每一个Cn的模都对应一个向量的模长,Cn的幅角主值对应向量的初始方向,而每一个nω都对应一个向量的旋转角速度,t是时间。n是整数,我没说他是自然数。每一个值都很重要,给你们举个反例:我一开始一不小心把所有的弧度制角度值不转角度制就直接写在数据包里,结果所有向量就清一色的排成扭曲程度不大的一串,一启动就画出下图里那些不成样的图形:

在Minecraft里我们就先summon所有向量:
- summon armor_stand ~ ~ ~ {CustomName:"{\"text\":\"VECTOR_n\"}",Marker:1b,CustomNameVisible:1b,NoGravity:1b,Rotation:[θnf,0f]}
注意所有的引号的转义!其中θn就是由Cn直接确定的角度制角度。然后我们执行绘制过程,也就是让一个实体绕着上一个实体作匀速圆周运动。方法有两种,一种是把一次性/tp到位,但你需要自己手算所有因为旋转而产生的相对偏移量,最大的缺陷是容易因为误差导致实体跑偏(没意外的话如果椭圆解多了直觉应该就是这种思路);另一种方式是先转动再/tp,优势是能更准确地保证半径,缺点是命令数目成倍增长。
我个人推荐第二种,具体实现:首先让所有被标记的、参与构成向量的实体旋转nωΔt度,然后将自己原本指向的NEXT实体/tp到离自己|Cn|远的地方。
- execute as @e[...] at @s run tp @s ~ ~ ~ ~nωΔt ~
- execute as @e[THIS] at @s run tp @e[NEXT] ^ ^ ^|Cn|
好了,现在,你需要解决的问题是:怎么求所有向量的模|Cn|、所有向量的初状态arg(Cn)、所有向量的角速度nω。如何根据已有曲线解析式解出你需要的一堆参数,感兴趣的童鞋可以阅读这个PDF:
SVG傅里叶变换结果转成复数对.zip (752.03 KB, 下载次数: 0)
自己写的,写的很烂,但是能用;不把文字直接写在帖子里,因为太长了,这个帖子主要讲大思路……
推荐3B1B的讲解视频:
https://www.bilibili.com/video/BV1vt411N7Ti
做这玩意需要的知识点:解椭圆(必须),寻找最佳参数方程(必须),解矩阵(必须),读SVG指令(必须),复变函数(必须,基础性质的话用你的脑洞去猜,八成是对的),会Illustrator(可选),撸代码(可选),操作数学软件(可选)。
提升数据包的工作效率
推荐阅读:https://www.mcbbs.net/thread-891687-1-1.html
首先我们应该明白我们的数据包的性质:选择大量实体,每一个实体都拥有不同的标记,对单个实体执行的指令相当单一。
为了提升效率你有这几个种思路:
- 减少单tick执行循环次数:选实体时总会遍历全实体初步筛选出一部分实体,再对该部分继续筛选。初步筛选时会考虑实体类型(筛掉类型不对的实体),但如果你敲过代码就应该知道筛选的条件语句管你是不是true都会执行,因而可以考虑在绘制流程中@e选择时加入type=...限定。
- 减少单次循环长度:见的不多,主要是指if/else选择执行的语块。这个可以完全忽略掉。
- 减少其他不必要的计算:比如将实体选择为药水云、隐形盔甲架,可能会节省部分系统资源。我自己的电脑上测试效果不明显。
个人实测结果:强制选择实体类型 + 隐藏模型,漏刻由1000+降到800(就是Server thread经常叫唤Can't keep up!什么什么的,那个表明你tps太低了)
一种列写参数方程的思路
思路直接来源于贝塞尔曲线的表达式。先明白一点,二维平面上的点都可以表示为二维向量。
现在假设我们就有起点B0,终点Bn,中间还有一堆控制点Bk。我们就把所有控制点Bk全部转换成二维向量,那么这些点构成的贝塞尔曲线表达式为:

每一个二维向量均未进行乘方运算,因而上式成立。
没错就是这些1-t和t直接把一大段函数封装进[0,1]或者说是[k,k+1]这样的区间里面了。注意到:t=0时只有第一项B0的系数不是零,t=1时只有最后一项Bn系数不是零,照这样说t取(0,1)区间里的值时应当表示出整段贝塞尔曲线。这样的优点就是写程序的时候节省一大堆写接口控制器的代码,缺点是长曲线画笔移速过快。
仿照贝塞尔曲线解析式,直线方程可以写成这种格式:y = A(1-t) + bt;事实上本来就有C10=C11=1;高次函数照样。
但是应该注意到t不一定作为底数出现,但是不管t在哪里,解决方法仍然如此。有个有点难理解的是椭圆表达式,办法还是打成参数方程:
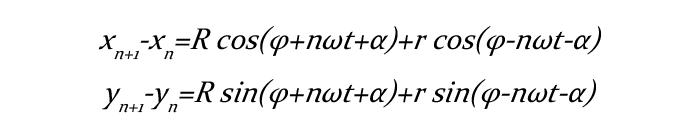
这里面你应该都发现φ+nωt+α和φ-nωt-α是线性的,所以只要找到起点和终点对应的角度A0和A1,再把时间函数写成上面那样的,就容易理解了。
对于其他类似情形,只要其时间关系能够满足f = f(kt + b)的格式,都可以用类似方法封装为f = f(b(1 - t) + (k + b)t)的格式。
原函数的最简单来源:SVG的Path
说他最直接,因为你可以到处都找得到,或者干脆自己做……
目前,市面上流行的SVG Path中的d属性通常有10种指令:位移指令M,直线指令L/H/V,贝塞尔曲线指令C/S/Q/T,椭圆弧段指令A,闭合指令Z。每一种指令都有绝对坐标和相对坐标两种模式,其中绝对坐标的指令头为大写字母,相对坐标的指令使用小写字母;指令一般总是继承上一指令的终点绝对位置。
指令的介绍与用法自行百度,或者查看W3C制定的SVG语法标准。我在这里仅列出一些注意事项。
MDN上的SVG教程:
https://developer.mozilla.org/en-US/docs/Web/SVG/Tutorial/Paths
| 指令类型 | 指令名称 | 指令简介 | 参数数量 | 兼容连用 | 注意事项 |
| 坐标控制指令 | M/m | 移动绘制点到某处 | 2 | 无意义 | 可能产生间断点,一般作为起始指令使用 |
Z/z | 关闭曲线 | 0 | 否 | 一般作为终止指令使用,但也有例外情形 | |
| 直线指令 | L/l | 绘制直线到某处 | 2 | 是 | - |
H/h | 绘制水平线到某处 | 1 | 无意义 | - | |
V/v | 绘制垂直线到某处 | 1 | 无意义 | - | |
| 贝塞尔曲线指令 | C/c | 绘制三次贝塞尔曲线到某处 | 6 | 是 | - |
S/s | 绘制三次贝塞尔曲线到某处 | 4 | 是 | 若上一指令为C/c/S/s,则第一控制点继与上一指令的第二控制点关于上一指令终点对称 | |
Q/q | 绘制二次贝塞尔曲线到某处 | 4 | 是 | - | |
T/t | 绘制二次贝塞尔曲线到某处 | 2 | 是 | 若上一指令为Q/q/T/t,控制点继与上一指令的控制点关于上一指令终点对称 | |
| 椭圆弧段指令 | A/a | 绘制椭圆弧段到某处 | 7 | 是 | 详见附件,特别多 |
| 兼容连用:指SVG指令中,如果连续两条指令类型相同、同使用绝对坐标或者同使用相对坐标,则后者的指令标识字母可以省略不写。此时指令将表现为参数数目翻倍,但是本质上仍是多条独立指令,不影响执行结果。 | |||||
| 间断点:原函数不连续产生的结果。在间断点处,原函数并不连续,但是拟合函数却是定义域内连续的,此时大量向量可能旋转到相似方向并快速甩头甩尾。学术上将其称之为吉布斯效应。 | |||||
 SVG椭圆解析的doc.zip
(309.6 KB, 下载次数: 0)
SVG椭圆解析的doc.zip
(309.6 KB, 下载次数: 0)
可视化的吉布斯效应,几个月前我的签名档GIF,注意突起的尖端:

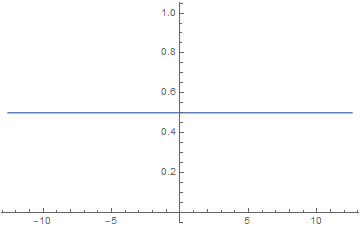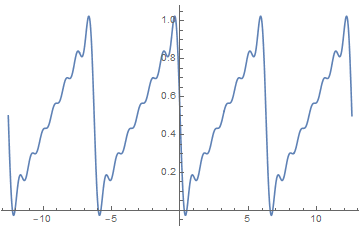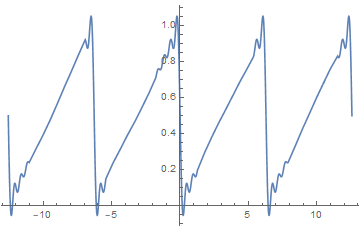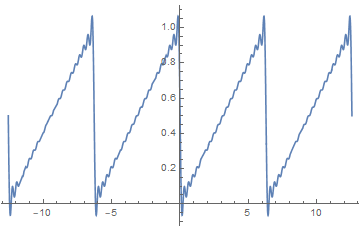
自己写的SVG Path解析程序和数据包
源码仓:https://github.com/Classault/MinecraftEntityFourier
毕竟还打算写成类库的
程序依赖jopt-simple5和Digester3,自行添加到classpath里面再启动
上面的一方通行数据包:
demopack.zip (21.03 KB, 下载次数: 0)
不会自动平整地形,自己创建超平坦或者/fill或者WorldEdit去//set。
程序参数:
| 参数名 | 类型 | 单位 | 必须 | 释义 | 默认值 |
| d | String | - | 否 | 一段SVG路径 | 内置路径 |
| directlyFrom | File | - | 否 | 直接包含SVG路径属性的文本文件路径,可为相对路径 | - |
| svg | File | - | 否 | SVG文件路径,可为相对路径 | - |
| namespace | String | - | 是 | 自定义数据包命名空间 | - |
| dataPackName | String | - | 是 | 自定义数据包名 | - |
| size | int | 百分比 | 否 | 尺寸缩放比例。比如值为55表示放缩至原尺寸的55% | 100% |
| level | int | 级 | 否 | 积分到多少级 | 255级 |
| angluarVelocity | int | 百分比 | 否 | 最低角速度,当为100%时最后一个向量每刻旋转1弧度 | 100% |
| precise | int | 级 | 否 | 定积分精度 | 16384级 |
| entity | String | - | 否 | 作为矢量起点和终点的实体 | 盔甲架 |
| block | String | - | 否 | 担当“墨水”的方块 | 石英块 |
该程序生成数据包的指令说明:
| 函数名 | 函数用途 | 调用函数 |
| <namespace>:init | 初始化,创建所有向量和计分板项 | - |
| <namespace>:start | 开始绘制 | - |
| <namespace>:stop | 停止绘制 | - |
| <namespace>:spy | 让玩家持续悬停于画笔正上方 | - |
| <namespace>:escape | 让玩家脱离画笔,恢复自由移动 | - |
| <namespace>:unload | 卸载数据包,清空所有向量实体和计分板项 | clear |
| <namespace>:clear | 清空向量实体 | - |
| <namespace>:main | tick.json执行的主函数,用户不要手动执行 | draw rotate follow |
| <namespace>:draw | 由main函数自动调用,用户不要手动执行 | - |
| <namespace>:rotate | 由main函数自动调用,用户不要手动执行 | - |
| <namespace>:follow | 由main函数自动调用,用户不要手动执行 | - |
用Java计算这个是真的强
才发现当时那个帖子放错文件了,我可真是个憨憨

才发现当时那个帖子放错文件了,我可真是个憨憨
本帖最后由 天佑酱 于 2020-8-28 00:25 编辑
互联网无时无刻不在告诉我 我是个废 。物
↖连傅里叶级数都不懂的屑
感觉楼主很喜欢数学的样子
互联网无时无刻不在告诉我 我是个废 。物
↖连傅里叶级数都不懂的屑
感觉楼主很喜欢数学的样子
玩java 的大佬真的强